Horizontal asymptote rules

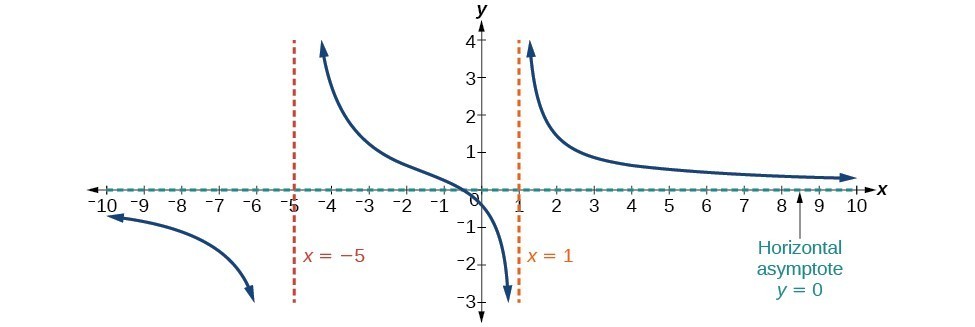
Asymptotes are imaginary lines that are very close to the total graph of a function or a part of the graph. Asymptotes are very useful when graphing a function because they help you think about which lines the curve should not cross.

A function’s horizontal asymptote is a horizontal line with which the function’s graph appears to coincide but does not actually coincide. The horizontal asymptote is used to determine the function’s end behaviour.

Horizontal asymptote definition

Before we get into the definition of a horizontal asymptote, let’s define a function. A function is an equation that shows the relationship between two things.

Functions typically explain the relationship between y and x. Functions are frequently graphed to provide a visual representation.

A horizontal asymptote is a line that shows how a function will behave at the extreme edges of a graph. The function can come close to, and even cross, the asymptote.

Horizontal asymptotes exist for functions with polynomial numerators and denominators. We know these as rational expressions. Let us take a look at one to see how a horizontal asymptote looks.

As a matter of fact, our function is a two-polynomial product. y = 0 is our horizontal asymptote. Examine how the function’s graph approaches the ends of the graph and gets closer and closer to that line. We can plot some points to see how the function behaves at its extremes.

Do you notice how, at the very far edges, the function gets closer and closer to the line y = 0? This is how a function behaves around if it has a horizontal asymptote. Horizontal asymptotes do not exist for all rational expressions. Let us now discuss the rules of horizontal asymptotes to see when and how a horizontal asymptote will exist.

Horizontal asymptotes follow three rules depending on the degree of the polynomials involved in the rational expression. Before we start, let’s define our function as follows:

On top of our function is a polynomial of degree n, and on the bottom is a polynomial of degree m. These degrees serve as the foundation for our horizontal asymptote rules.

Try comparing the degree of the numerator “M” to the degree of the denominator “N” to find horizontal asymptotes.

If M is less than N, then y=0 is the horizontal asymptote
M is greater than N, then, no horizontal asymptote
If M is equal to N, then divide the leading coefficients
When n is less than m, the horizontal asymptote is y = 0, which corresponds to the x-axis.

When n equals m, then the horizontal asymptote is y = a/b.

There is no horizontal asymptote when n exceeds m.

The degrees of the polynomials in the function determine whether or not a horizontal asymptote exists and where it is located. Let’s look at how we can apply these rules to find horizontal asymptotes.

To understand horizontal asymptote rules, you must remember these.

Horizontal asymptote rules rational functions

A rational function can only have one horizontal asymptote. Though we can use the limits to find the horizontal asymptotes, the following tricks are an easier way to calculate the horizontal asymptotes of rational functions:

The function has no horizontal asymptote if the degree of the numerator is greater than the degree of the denominator.

Again, if the degree of the denominator is greater than the degree of the numerator, the function has one horizontal asymptote, which is y = 0.

Similarly, if the numerator’s degree equals the denominator’s degree, the function has one horizontal asymptote, which is y = the ratio of the numerator’s and denominator’s leading coefficients.

Suppose, f(x) = 2x / (x – 3), the degree of the numerator equals the degree of the denominator (= 1). As a result, the horizontal asymptote of f(x) is y = 2/1 = 2.

Horizontal asymptote rules for limits

A function f(x) will have the horizontal asymptote y=L if either or . So, to find horizontal asymptotes, we simply evaluate the function’s limit as it approaches infinity, and then again as it approaches negative infinity. A function can only have two horizontal asymptotes — one in each direction.

To understand horizontal asymptote rules, you must remember these.

Horizontal asymptote rules exponential function

An asymptote is a line that a function’s graph approaches as x increases or decreases without bound. Moreover, an exponential function’s horizontal asymptote indicates the function’s value limit as the independent variable becomes extremely large or extremely small.

Suppose, an exponential function is of the form

Thus, it has the following properties:

The function has a one – to – one relationship.
The function’s horizontal asymptote is given by y = 0.
Its domain is (- , )
Its range is (0 , )
There is no x intercept
The y intercept is (0 , 1)
The function is increasing if b is greater than 1 and decreasing if b is less than 1

There is always one horizontal asymptote for an exponential function. The parent exponential function is of the form f(x) = bx, but transformations can change it to f(x) = abkx + c. The horizontal asymptote is represented by ‘c’, which is the vertical transoformation of the parent exponential function. To sum up:

The horizontal asymptote of f(x) = bx is y = 0.
y = c is the horizontal asymptote of f(x) = ab^kx + c.

Horizontal asymptote rules: degree

A horizontal asymptote is a horizontal line that is not part of the graph of a function.

However, it guides it for x-values that are at the far right and/or at the far left. The graph may cross it, but for big and small enough x values (approaching ±∞), the graph will eventually get closer and closer to the asymptote without touching it. A horizontal asymptote is a type of slant asymptote.

Let deg N(x) be the numerator’s degree and deg D(x) be the denominator’s degree.

So, if,

If deg D(x) is equal to deg N(x), then, y = (leading coefficient of N(x) / leading coefficient of D(x))
Again, if deg D(x) is less than deg N(x), then, y = 0, which is the x-axis
Also, if deg D(x) is greater than deg N(x), then, no horizontal asymptote exists.

Another way of finding horizontal asymptote for rational function is if we divide N(x) by D (x). If the quotient is constant, the equation of a horizontal asymptote is y = this constant.

To understand horizontal asymptote rules, you must remember these.

Horizontal asymptote rules: calculus

There are two ways by which you can find the value of horizontal asymptotes.

Method 1:

If or , then, we call the line y = L a horizontal asymptote of the curve y = f(x).

Method 2:

Suppose, f(x) is a rational function.

In this case, the horizontal asymptote is y = 0 when the degree of x in the numerator is less than the degree of x in the denominator.

Again, if the degree of x in the denominator equals the degree of x in the numerator, then y = c, where we obtain c by dividing the leading coefficients.

Horizontal asymptote calculator

Follow the instructions to use the calculator:

In the first step, in the given input boxes, enter the function with respect to one variable.
Step 2: To find an asymptotic graph for a given function, click the “Compute” button.
Finally, press the “Reset” button to clear the fields and locate the asymptotic graph for various functions.

Horizontal asymptote equation

It is very easy to find horizontal asymptote.

There is a horizontal asymptote at y = 0 if the degree of the denominator is greater than the degree of the numerator.

A slant asymptote is obtained by multiplying the degree of the denominator by the degree of the numerator.

If the denominator’s degree equals the numerator’s degree, there is a horizontal asymptote at y = c, where c is a constant.

You can aslo use limit to find this.

If or if , then, we call the line y = L a horizontal asymptote of the curve y = f(x).

Horizontal asymptote examples

A horizontal asymptote is a parallel line to which a portion of the curve is very close. However, keep in mind that a horizontal asymptote should never touch any part of the curve. But it may cross the curve.

Example 1:

Can you find the horizontal asymptote of y = (5x³ + 7x) / (x+5).

Solution:

The degree of the numerator in this case = 3.

The degree of the denominator = 1.

As a result, the numerator’s degree is seen to be greater than the denominator’s degree.

So f(x) has no horizontal asymptote.

Answer: This function has no horizontal asymptote.

Example 2:

Use the horizontal asymptote rules and figure out the value of c if horizontal asymptote of f(x) = 2x – c is y = 5.

Solution:

We know that the horizontal asymptote of an exponential function is determined by its vertical transformation.

So the horizontal asymptote of f(x) = 2x – c is y = -c.

But it is given that the horizontal asymptote of f(x) is y = 5.

Thus, -c = 3 (or) c = -5.

Answer: k = -5.

Example 3: Find the horizontal asymptote of (10x² – 7x) / (5x² – 2x + 3)

Solution:

We must first compare the degrees of the polynomials. Both the numerator and denominator are polynomials of the second degree. Because they are of the same degree, the coefficients of the highest terms must be divided.

The coefficient of the highest term in the numerator is 10.

The coefficient of the highest term is understood in the denominator as 5.

10 / 5 = 2

Answer: Thus, at y = 2, the horizontal asymptote is reached.

Example 4:

Calculate the horizontal asymptote of the function f(x) = 10x / (x – 5).

Solution:

= 10x / (x – 5)

Which is = 10x / [x (1 – 5/x) ]

= 10 / (1 – 5/x)

= 10 / (1 – 0)

= 10

So y = 10 is the horizontal asymptote of the function. Now we will look for the other limit.

= 10x / (x – 5)

Which is = 10x / [x (1 – 5/x) ]

= 10 / (1 – 5/x)

= 10 / (1 + 0)

= 10

Again, we have 2 which gives the same horizontal asymptote to be y = 10.

Therefore, the function has only one horizontal asymptote which is y = 10.

Horizontal asymptote and vertical asymptote

Because an asymptote is a horizontal, vertical, or slanted line, its equation is x = a, y = a, or y = axe + b. Here are the rules for determining all types of asymptotes for the function y = f(x).

A horizontal asymptote has the formula y = k, where x tends to or x tends to – . It is the value of one or both of the limits and .

A vertical asymptote is defined as x = k where y tends to or y tends to -.

A slant asymptote is defined as y = mx + b, where m 0. An oblique asymptote is another name for a slant asymptote. It is usually present for rational functions, and mx + b is the quotient obtained by dividing the rational function’s numerator by the denominator.

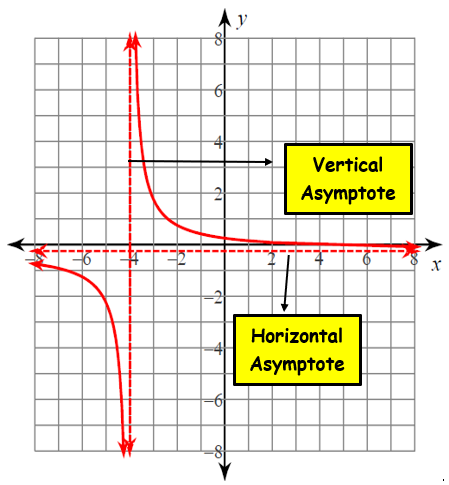
Can a horizontal asymptote cross the curve?

Yes, a horizontal asymptote y = c of a function y = f(x) can cross a curve or a graph. In other words, there may be an x value such that f(x) = k. This is not true for any vertical asymptote because a vertical asymptote never intersects the curve. Here’s an illustration of the horizontal asymptote (HA) intersecting the curve.

Horizontal asymptote rules FAQs

1. Is it possible to have more than one horizontal asymptote for a function?

No, a function can’t have more than two horizontal asymptotes.

2. Why are graphs able to cross horizontal asymptotes?

At x=0, the graph crosses the x-axis. As x approaches infinity, it rises to a maximum value and then falls toward y= 0 as x approaches infinity. It decreases to a minimum value for x 0, then rises toward y=0 as x approaches negative infinity. Although y = 0 is a horizontal asymptote, the graph crosses y = 0 at x = 0.

3. How are vertical and horizontal asymptotes found?

Vertical asymptotes will occur at x values where the denominator is equal to zero: x 1=0 x = 1 As a result, the graph has a vertical asymptote at x = 1. To find the horizontal asymptote, we note that the numerator’s degree is two and the denominator’s degree is one.

4. Is it probable for a graph to cross a horizontal asymptote?

Note that, a common misconception among students is that a graph cannot cross a slant or horizontal asymptote. A graph can have asymptotes on both the vertical and horizontal axes (sometimes more than once). A graph cannot cross those vertical asymptote critters. This is because these are the domain’s weak points.

5. How do you find an equation’s asymptote?

Vertical asymptotes are found by solving the equation n(x) = 0, where n(x) is the denominator of the function. It should be noted that this only works if the numerator t(x) for the same x value is not zero. With the equation x = 1, the graph has a vertical asymptote.

6. Which function does not have a horizontal asymptote?

When the degree of the numerator is greater than the degree of the denominator, a rational function has no horizontal asymptote. A) The degree of the numerator is less than the degree of the denominator in f(x)=7x-2/10x². B) In f(x)=x-1/3x, the numerator has a lower degree than the denominator.

7. How do you find a function’s vertical asymptote?

Simply set the denominator to 0 and solve for x to find the vertical asymptote(s) of a rational function.

8. In exponential functions, what is a horizontal asymptote?

An asymptote can be vertical, oblique, or horizontal in orientation. Horizontal asymptotes are the values that the curve approaches as x becomes very large or very small. Any function in which the independent variable takes the form of an exponent; they are the inverse function of logarithms.