Derivatives are crucial topics in mathematics. Moreover, derivatives offer a wide range of applications in practically every field of engineering and research. Then, derivative identifies the maximum and lowest values of a function, as well as to forecast the monotonicity of a given function.
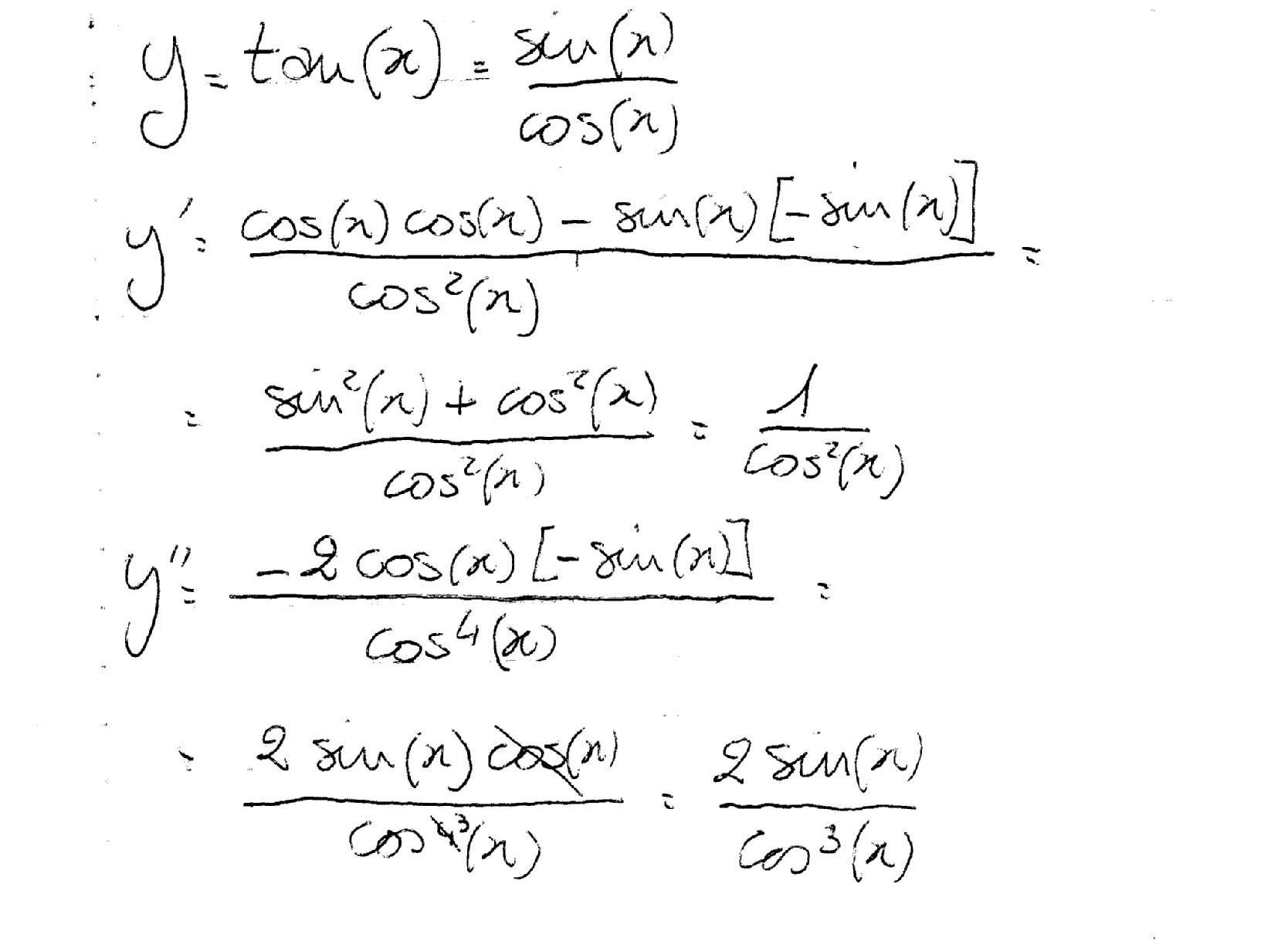
Then, the square of sec x is the derivative of tan x. Before we go there, let’s go over some tan x facts. Then, tan x is the ratio of the opposing side of x to the adjacent side of x in a right-angled triangle, and it can thus be expressed as (sin x)/ (cos x). Then, this is uses in the differentiation of tan x. In this article, we are talking about this derivative. So, please keep reading to know more about it.
Derivative of Tangent x
Moreover, let F be a real-valued function with an open interval (a,b). Then, this indicates that the interval (a,b) is now serving as the domain of F. Then, the real number, on the other hand, indicates that the range of F is a subset of the collection of all drills.
Moreover, every tiny X exists inside the open interval F of X. This is the current set of valid inputs for machine F. However, because F is real-valued, X exists as a real number. As a result, any X in the interval (a,b) of X exists as a real number. However, (a,b) is the domain of all the points for which F is defined, and F of X is nothing more than the range of real numbers.
Read Also: Hypotonic Definition and Hypotonic Solution Example
An angle’s tangent is the opposite of adjacent. The tangent, on the other hand, is the only trig ratio that does not employ the hypotenuse sign. A Tangent line, on the other hand, is a line that is tangent to a curve. It now means that it only touches the curvature at one place. Then proceed in either direction with the exact slope of the curve at the point. The tangent line, on the other hand, is not parallel to the curve; its slope simply matches the slope of the precise point on the curve. The tangent line, on the other hand, is useful since it can tell you the rate of change of a curve at a certain location.
Derivative of Tangent x Proof
Tangent x and cosines are related in that we can conduct right-hand genetics by saying x over cosine x. This, however, is equivalent to taking sine x over cosine x. The following function(g) is the first side, which is cosine x. The top function(f) is thus equal to sine x. However, sine x’s root equals cosine x, thus f is prime and will be cosine x. Then, for the numerator, we’ll choose cosine x, which is times cos x. However, we must remove cosine x times cosine, followed by the war potion rule. So we require sine x multiplied by negative sine x.

This cosine x times cosine x will be cosine squared x and minus sine x times negative sine x on top. Now we have two sciences multiplying each other, which is why it’s sine squared x. However, one cosine squared x plus sine squared x is only one, thus we only have one on the bottom. Now we have cosine x followed by square. However, this implies that it is cosine squared x. We do, however, know that one over cosine equals secant squared x.
Derivative of Tangent x formula
The derivative of tan x with respect to x is represented by d/dx (tan x) (or) (tan x)’ and equals sec2x. Tan x is distinct in its domain. We utilize existing trigonometric identities and differentiation methods to establish the differentiation of tan x to equal sec2x. This may be demonstrated in the following ways:
- First-principles proof
- The chain rule provides proof.
- Proof using the quotient rule
The formula for tan x differentiation is,
d/dx (tan x) = sec^2x (or)
(tan x)’ = sec^2x
d/dx (tan x) = sec^2x
Derivative of Tangent x using first principle
To calculate the derivative of tan x, we first assume that f(x) = tan x. Then, by first principle, its derivative is supplied by the limit stated below.
Lim h tends to 0 = f'(x) [f(x + h) – f(x)] h… / h.. (1)
Because f(x) = tan x, f(x + h) = tan (x + h).
Using these in place of (1),
f'(x) = limₕ→₀ [tan(x + h) – tan x] / h
Then, = limₕ→₀ [ [sin (x + h) / cos (x + h)] – [sin x / cos x] ] / h
Then, = limₕ→₀ [ [sin (x + h ) cos x – cos (x + h) sin x] / [cos x · cos(x + h)] ] / h
By sum and difference formulas, sin A cos B – cos A sin B = sin (A – B).
f'(x) = limₕ→₀ [ sin (x + h – x) ] / [ h cos x · cos(x + h)]
Then, = limₕ→₀ [ sin h ] / [ h cos x · cos(x + h)]
Then, = limₕ→₀ (sin h)/ h · limₕ→₀ 1 / [cos x · cos(x + h)]
According to limit formulae, lim h tends to 0 (sin h)/ h = 1.
f'(x) = 1 [ 1 / (cos x · cos(x + 0))] = 1/cos2x
We know that the reciprocal of cos is sec. So,
f'(x) = sec2x.
So, as a result, proven.
Derivative of Tangent x using chain rule
We shall use the chain rule to demonstrate the differentiation of the tan x formula. Let us remember that y = tan x may be written as y = 1 / (cot x) = (cot x)-1. Now, according to the power and chain rules,
y’ = (-1) (cot x)
Then, -2 · d/dx (cot x)
We may deduce that d/dx (cot x) = -csc2x. Furthermore, a-m = 1/am due to an exponentiation feature.
y’ = -1/cot2x · (-csc2x)
Then, y’ = tan2x · csc2x
Now, tan x = (sin x)/(cos x) and csc x = 1/(sin x). So
Then, y’ = (sin2x)/(cos2x) · (1/sin2x)
Then, = 1/cos2x
We have 1/cos x = sec x. So
y’ = sec2x
So, as a result, proven.
Derivative of Tangent x using quotient rule
However, we may use the quotient rule to get the derivative of tan x. Then, we must express tan x as a fraction for this. Then, we already know that tan x = (sin x)/ (cos x). As a result, we suppose that y = (sin x)/ (cos x). Then, using the quotient rule,
y’ = [ cos x · d/dx (sin x) – sin x · d/dx (cos x)] / (cos2x)
Then, = [cos x · cos x – sin x (-sin x)] / (cos2x)
Then, = [cos2x + sin2x] / (cos2x)
According to one of the Pythagorean identities, cos2x + sin2x = 1.
(cos2x) = sec2x y’ = 1
As a result, proven. This demonstration is the simplest of all the proofs of the derivatives of tan x.
Derivative of Tangent x ^2
We are squaring the tangent of x, which is a function. We now set u equal to the tan of x. Then the tangent squared of x is the tangent of x. All of this is now squared, which equals u squared. When it comes to distinguishing a composite function of a function, though. The chain rule must then be applied. Now, dy/dx equals dy/du multiplied by du/dx.
The function y is equal to the tangent of x all squared in this situation. On the other hand, dy/du is two u; we bring down the strength of u and then remove one. The du/dx is therefore equal to the derivative of x’s tangent, which is equal to x’s secant squared. We now obtain dy/dx equal to two times u, which is the tangent of x divided by the secant squared of x. The derivative, often known as the derivative of the tangent squared of x, is equal to 2 secants squared of x multiplied by the tan of x.

We may proceed by employing the chain rule.
It says that y = f(g(x)) for any function.
=> d/dx ( f(g(x) ) = f’ (g(x)) · g’ (x)
Given y = tan2x
dy/dx = (2 tan x) × (dy/dx(tan x))
= 2 tanx sec2x
Derivative of Tangent x other method
We have the tan square x derivative. Assume that y equals tan square x. Differentiate with respect to x, and the derivative of tan square x equals dy upon dx. Now it’s tan x full square on d tan x into d tan x on dx. It will be two tan x times sec squared x once we use the xn formula. As a result, the derivative of tan square x is two tan x sec squared x.
Let, y = tan^2x
dy/dx = d/dx (tan^2x) = d(tanx)^2 /d(tanx) times d(tanx)/dx
Next, dy/dx= 2 tanx times sec^2x
Next = dy/dx = 2tan sec^2x.
Derivative of Tangent x ^3
Assume f(x)=tan^3(x)
f(x) can be expressed as a composite function:
Assume g(x)=x^3 and h(x)=tan (x)
f(x)=g(h(x))
Using the chain rule, we can deduce that
f′(x)=g′(h(x))
⋅h′(x)
Consider the following to determine g′(h(x)):
g′[h(x)]=limx→0g(h(x)+Δx)+g(h(x)) /Δx
Simply replace all of the x’s in the formula with h(x), as it is now the new value of the function at which the limit is being taken. You may see that this is the same as
d/d[tan(x)] tan3(x)
According to the power rule,
d/dx x^3=3x^2
As a result of the power rule,
d/d[tan(x)] tan^3(x)=3tan^2(x)
g′[h(x)]=3tan^2(x)
h′(x)=sec2(x)
Derivative of tangent x ^-1
The tangent of x is the secant of X squared. Now, y equals the inverse tangent of x, which is equivalent to asserting that the tangent of y equals X. We need the derivative of both sides in relation to X.
The chain rule must now be applied. Secant squared of y is the derivative of the tangent of y with respect to y. The cosine of y squared, on the other hand, is a similar type function. When using the chain rule, it will be the derivative of y’s tangent with respect to y.
Now, it times the derivative y with respect to x. On the right-hand side, the derivative of x with respect to x will be equal to one. Now we need to multiply both sides times the cosine of y squared. Then we get the derivative of y with respect to x equal to the y squared cosine. Let’s divide by one; the one is equal to the sine squared of y plus cosine squared of y.

Now multiply one over the cosine and divide the numerator by the cosine square of y. Next, those characters are just going to have one. And the denominator is going to be equal to one. Then we are going to have sine squared y over cosine squared y.
This, however, is the same as the sine of y divided by the cosine of y.
The sum of the squares is one over one plus the tangent of y squared. This will then be one over one plus the tangent of y, which equals x squared. This is now equal to one plus one plus x squared.
Note
- d/dx (tan x) is NOT the same as d/dx(sin x) / d/dx (cos x). To get the derivative of tan x, we must utilize the quotient rule (written as (sin x)/(cos x)).
- d/dx (tan x) is NOT the same as cot x. The reciprocal of tan x is cot x.
- Tan x and tan-1x derivatives are NOT the same.
- sec2x d/dx(tan x) = sec2x
- d/dx(tan-1x) = 1/(1 + x2)
Derivative of tangent x+y
y = tan(x+y) , differencing with regard to x and employing the chain rule
dy/dx = d/dx { tan (x+y)}*d/dx (x +y)
or, dy/dx = sec^2(x+y) {1+dy/dx}
or, dy/dx – sec^2(x+y)dy/dx = sec^2(x+y)
Then, dy/dx = sec^2(x+y)/{1 – sec^2(x+y)}
or, dy/dx = sec^2(x+y)/{-(tan^2(x+y)}
or, dy/dx = – 1/ sin^2(x+y) = – cosec^2(x+y)
Derivative of tangent x ^ cot x
Moreover, let y equals tan x to the power cot x. Then, the first method, a to the power b equals to e to the power b log a. So, y equals to e to the power cot x log tan x. Then, differentiate with respect to x, dy upon dx equals to e to the power cot x log tan x into differentiate cot x into log tan x. Now, We will use the product rule. Then we get tan x to the power cot x times cot x into the differentiation of log tan x plus log tan x into the differentiation of cot x.

Now, it equals tan x to the power cot x into cot x times 1/tan x into sec square x plus log tan x into minus cos square x. Then, it will be tan x to the power cot x, and in the third brackets, cos x/sinx into cos x/sin x into 1/cos^2x minus log tan x into cosec^2x. Now we are canceling the cos x. Then dy/dx equals tan x to the power cot x into cosec square x minus cosec square x into log tan x. After some calculation, the answer is tan to the power cot x into cosec^2x into one minus log tan x.
Let, y=tanx^cot(x)
Then, log y = log tan(x)^cot(x)
Then, log y= cot(x).log(tanx).
Next, 1/y.dy/dx=cotx.(1/tanx).sec^2x-cosec^2x.log tanx.
Next, 1/y.dy/dx=cosec^2x-cosec^2x.log tan x
Now, dy/dx=y.cosec^2x (1-log tanx)
Now, dy/dx=tanx^cotx.cosec^2x.(1-log tan x)
Derivative of Tangent x examples
Derivative of Tangent x example 1
What is the derivative of tan x in terms of sec x?
Solution:
Let v equal tan x and u equal sec x. Then dv/dx is sec2x, and du/dx equals sec x tan x.
We must locate dv/du We can write this as
dv/du = (dv/dx) / (du/dx)
Then, = (sec2x) / (sec x · tan x)
= (sec x) / (tan x)
Then, = (1/cos x) / (sin x/cos x)
Then, = 1/sin x
Atlast, = csc x
The derivative of tan x with respect to sec x is csc x.
Derivative of Tangent x example 2
Find the derivative of tan x · sec2x.
Solution:
Let f(x) = tan x · sec2x.
By product rule,
f'(x) = tan x · d/dx (sec2x) + sec2x · d/dx(tan x)
= tan x · (2 sec x) d/dx (sec x) + sec2x (sec2x) (by chain rule)
Then, = 2 sec x tan x (sec x tan x) + sec4x
= 2 sec2x tan2x + sec4x
The given function’s derivative is 2 sec2x tan2x + sec4x.
Some frequently asked questions
How do you find the derivative of tangent?
1) Determine the first derivative of f. (x). 2) Enter the specified point’s x value into f ‘(x) to determine the slope at x. 3) Input the x value into f(x) to determine the tangent point’s y position. 4) Using the point-slope formula, combine the slope from step 2 with the point from step 3 to derive the equation for the tangent line.
What is the derivative formula?
The derivative of a function of a real variable measures the quantity’s sensitivity to change as defined by another quantity. The Derivative Formula is as follows: f 1 (x) = lim delta x tends to 0 f (x + delta x) f (x) x.
What is the differential of sec x?
Sec x tan x is the derivative of sec x with regard to x. That is, it is the sum of sec x and tan x. The derivative of sec x with respect to x denoted using d/dx(sec x) (or) (sec x)’. As a result, d/dx (sec x) = sec x tan x.
What are the formulas of derivative tan x?
The derivative of tan x with respect to x is represented by d/dx (tan x) (or) (tan x)’ and equals sec2x. Tan x is distinct in its domain. We utilise existing trigonometric identities and differentiation methods to establish the differentiation of tan x to equal sec2x. This may be demonstrated in the following ways:
- First-principles proof
- The chain rule provides proof.
- Proof using the quotient rule
What is the derivative of CSC X?
csc x (cot2x + csc2x) is the double derivative of csc x. The double derivative is just the second derivative of a function. We can get it after differentiating the first derivative of csc x.
What is tangent?
An angle’s tangent is the opposite of adjacent. The tangent, on the other hand, is the only trig ratio that does not employ the hypotenuse sign. A Tangent line, on the other hand, is a line that is tangent to a curve. It now means that it only touches the curvature at one place. Then proceed in either direction with the exact slope of the curve at the point. The tangent line, on the other hand, is not parallel to the curve; its slope simply matches the slope of the precise point on the curve. The tangent line, on the other hand, is useful since it can tell you the rate of change of a curve at a certain location.
What is the derivative of 2x?
The derivative of 2x equals 2 because the formula for the derivative of a straight line function f(x) = axe + b is f'(x) = a, where a and b are real values. The formula d(ax+b)/dx = an used to compute 2x differentiation.
What is the derivative of sec x tan x?
According to the Sum Rule, the derivative of sec(x)+tan(x) with regard to x is ddx[sec(x)]+ddx[tan(x)] d d x [ sec ( x ) ] + d d x [ tan ( x ) ] . The derivative of sec(x) with respect to x is sec(x)tan(x) sec ( x ) tan ( x ).
What is the derivative of 6?
Because 6 is constant in relation to, the derivative of 6 in relation to is 0.