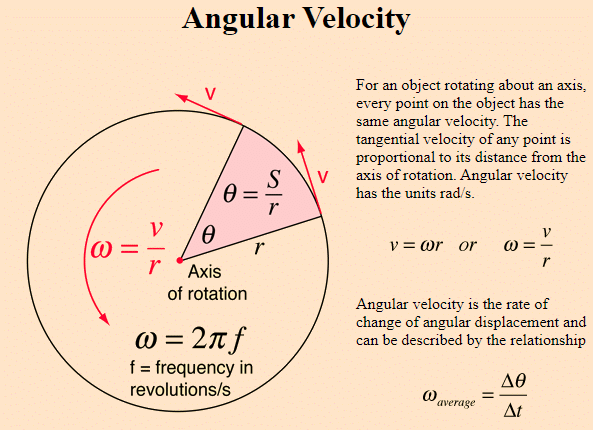
Angular velocity describes the rotating movement of bodies. It measures how quickly they travel around a point of rotation. There are two types of rotations to consider. The first explains the motion of an object’s centre of mass around a specified point in space, characterised as an origin. Planets orbiting the Sun are two instances, as does an automobile exiting the freeway. We write angular velocity as AV.
The second describes the rotation of the body around its own centre of mass, familiar as the spin. So, the quantum property of particles has another name which is spin. You’ve probably seen a basketball player twirl a ball on his finger. In general, the higher the AV, the quicker the movement. In this article, we are talking about this formula. So, keep reading to know more about it.
Angular velocity formula
ω = 2 pi N over 60 rad per second is the AV formula. We know that the velocity formula in linear motion is the general formula; velocity is just the distance upon the time. If your heart beats twice in one second, the velocity of your body in linear motion is two minutes per second. Assume we apply this approach to angular motion as well, thus the angular displacement unit per second time. So, if your body is rotating, let N be the rpm of the body. The rpm abbreviation stands for rotations per minute. If we want per second, we must divide by 60.
Because one minute contains 60 seconds, and revolutions per minute converted to seconds by dividing by 60. We know that the body turns one complete revolution, covering 360 degrees, which is equal to 2 pi radians. It will be N revolution if you take 1 minute. N revolution is equal to 2 pi upon N radians. Then you divide one second by 60 radians per second. So, this is 2 pi N upon 60 radians per second. We obtained the AV formula, ω = 2 pi N divided by 60.
ω= 2πN/60 rad/s
Because an object’s AV is its angular displacement with respect to time. AV represented as follows:
ω= θ/t
Where ω is the AV, θ is the angular displacement, and t is the time change. Positive AV denotes counterclockwise rotation, whereas negative denotes clockwise rotation.
Angular velocity formula average
A rotating rigid body’s average angular velocity is the ratio of angular displacement to time interval.
ω average= delta θ/delta t
=θ 2 – θ 1/ t 1 – t 2
Angular velocity formula Instantaneous
The limit of the average AV as the time interval approaches 0 is the instantaneous angular velocity.
ω ins = limit delta t tends to 0 delta θ /delta t
=d θ/ dt
Angular Velocity Formula rpm
Revolutions per minute (rpm) and angular velocity, two measurements of how quickly a point spins around another point. These used to solve issues in physics, mechanical engineering, and computer programming. In engineering simulations and video games, rpm and AV are sometimes used interchangeably to mimic pulleys spinning and wheels rolling.
The term angular velocity refers to the rate at which a circular object, such as a wheel, spins. Because a circle has 360 degrees, a wheel that completes one complete rotation about its centre in one second will have an angular velocity of 360 degrees per second. Because it takes 60 seconds for the second hand of a clock to complete one complete circle around its centre, it has an AV of 360 degrees every 60 seconds, or 6 degrees per second.

Revolutions per minute also used to describe the rate at which a circular item, such as a wheel, spins. Because one revolution is equal to one complete rotation or spin around a central point. A wheel that makes one complete rotation about its centre in a minute to revolve at a rate of one revolution per minute, or 1 rpm. Because it takes one minute for the second hand of a clock to complete one complete revolution around its centre, it has a rotation rate of one revolution per minute, or one rpm.
Angular velocity to rpm conversion
One revolution is 360 degrees and there are 60 seconds per minute. AV in degrees per second translated to revolutions per minute by multiplying the angular velocity by 1/6. If the AV is 6 degrees per second, the rpm is 1 revolution per minute, since 1/6 multiplied by 6 equals 1.
Angular velocity formula in terms of linear velocity
Let v denote linear velocity and angular velocity. Initially, a body moves on a circular route with radius r, and subsequently its position changes from p to q. That is why θ is formed in the centre. θ, on the other hand, is angular displacement. We know that angular displacement θ = l divided by r. Then we may plug l equals r into θ. Now we must distinguish both sides in terms of time t.
As a result, we may convert dl/dt equal to r to d θ /dt where r is constant. Following that, dl/dt will be v and d θ /dt will be ω. Angular displacement, on the other hand, is now AV, while the rate of change of linear displacement by time is linear velocity. This is a scalar form, and we may write v = ω into r in vector form. Now, v denotes linear velocity, angular velocity, and r denotes radius vector or position vector.
Then, v= ⍵ ⨯ r.
Angular velocity formula in gravitation
The formula for angular velocity is ω = 2 pi upon T. We’ll assume it’s revolving in a circular motion. T, on the other hand, is nothing more than the amount of time it takes to spin. However, we know that one revolution of the Earth takes 24 hours. However, we must convert the hour to the minute. As a result, we must convert 24 hours, which equals 24, to 3600. ω is now equal to 2 pi on 86400.

ω=dθ/dt
Here,dθ=2πRadians
dt = 24Hours
Now, The SI unit of angular velocity is rad/sec
so we need to convert our time to seconds
Next, 1 hour = 3600 sec
⇒24 hours
=24×3600
=24×3600 sec
Now, ω=2π/24×3600 rad/sec
⇒ω=7.29×10^−5 rad/sec
Angular velocity formula in vector form
The angular velocity vector’s magnitude is just the rate at which it rotates – the angle swept out per unit time. The Greek letter ω (let’s call it “w” instead because I don’t have a Greek font!) is the sign for angular velocity. – and it is measured in radians per second.
However, it is difficult to “obtain” the direction of that angular velocity vector. Because the rotating object’s many sections are moving in separate directions. So the technique for determining the direction of the angular velocity vector is to allow it to be along the axis of rotation (despite the fact that nothing moves in that direction), with the direction of that vector following what is known as the “right-hand rule.”
That is, curl your right hand’s fingers with the sensation of rotation, and your right thumb will point in the vector’s direction. If the disc rotates as indicated in the picture, the right-hand rule states that the angular velocity vector should be upward and parallel to the axis of rotation.
Look at the preceding illustration of the disc rolling from left to right to see that this is unambiguous. Although it is unclear whether this is clockwise or counterclockwise depending on which side of the disc you are viewing it from, curling your right-hand fingers with the same sense of rotation as the disc, your right thumb points into the page – and it doesn’t matter which side you are viewing it from.
That is, the angular velocity vector would have a magnitude equal to the rotation rate of the disc and would have the right-hand rule’s direction.
Angular velocity formula circular motion
Circular motion is the movement of an item in a circular route. A race vehicle going around a circular curve, a toy linked to a thread swinging in a circle around your head, or the circular loop-the-loop on a roller coaster are all examples of circular motion. Spin is the rotation of an item on an axis that passes through its centre of mass, such as the Earth revolving on its axis, a wheel turning on its axle, the spin of a tornado on its path of destruction, or a figure skater spinning during an Olympic performance. Objects can spin while in circular motion, such as the Earth rotating on its axis while circling around the Sun, but we shall look at these two movements separately.
ω = r v / |r|^2, where all of these variables are vectors and |r| signifies the radius’s absolute value. In reality, the angular velocity is a pseudovector with a direction perpendicular to the plane of rotational movement.
Angular velocity formula dimension
ω = angular displacement divided by time is the dimensional formula for angular velocity. The SI unit for angular velocity is now the radian per second. θ is now a dimensionless quantity. If a particle has a radius of r and its starting location is p, the particle’s position will be p after some time period. The formula for angular displacement is arc upon radius. The arc length is denoted by s. As a result, θ = s divided by r. Nows measures the meter’s intern, and r also measures the meter’s intern. As a result, both metres will be cancelled, yielding a result of 1. M power zero, L power zero, and T power zero are the new dimensions of angular displacement. It is a quantity that has no dimensions.
So the angular displacement is expressed as 1 upon t, and because t is nothing but time, the SI unit of time is the second. When second is stated in terms of dimension T, ω = 1. T will now be the numerator, while T to the power minus 1 will be the denominator. The format of angular velocity in the dimensional formula is M to the power absent, L to the power missing, and T to the power minus 1.
Proof
Angular Velocity = Angular displacement × [Time]-1…(1)
Now, the dimensional formula of Angular displacement = [M^0 L^0 T^0]….(2)
And, the dimensions of time = [M^0 L^0 T^1]……(3)
Substituting equations (2) and (3) into equation (1) yields,
Next, angular Velocity = Angular displacement × [Time]-1
Or, v = [M^0 L^0 T^0] × [M^0 L^0 T^1]-1 = [M^0 L^0 T^-1]
The angular velocity, on the other hand, is dimensionally represented as [M^0 L^0 T^-1].
Angular velocity formula with radius
Assume we have an item that is travelling in a circular motion. As a result, the item is travelling in a circular path that resembles a centre clockwise circular path. The object is now rotating five times per second. However, radians are only one method of measuring angles. You might use degrees per second instead. If we do it in radians, we can see that each rotation is 2 pi radians. Next, if we move completely around a circle, we have travelled 2 pi radians. Because there is 2 pi each rotation, we can perform some dimensional analysis. Then we multiply 5 times 2 pi to get 10 pi radians per second. It also does the dimensional analysis and makes sense. If we are making five rotations per second, each revolution is two pi radians.
Read Also: Derivative of Tangent x: Formula, Rules, Examples
So we’re moving at a rate of 10 pi radians per second. So 5 revs/second or 10 pi radians/second are effectively measuring the same thing. Angular velocity, on the other hand, is a measure of how rapidly you are rotating around a central point. Then there’s angular velocity, which tells us how fast our angle is changing or the pace at which the angle is changing. However, angular velocity is sometimes confused with angular speed. Next, it is a vector quantity, and the fact that the vector is literally bursting out of the page is a bit perplexing. It is, however, a fictitious vector. So it’s a vector quantity, and the vector’s orientation is determined by which way it spins. There is a vector, for example, when it is rotating counterclockwise; the true angular vector does appear on the page.
Result
The angular velocity vector will appear on the page when it rotates clockwise. When we consider a two-dimensional plane, we may consider an angular velocity to be a pseudo-scalar. However, we may include it as a scalar quantity if we indicate which way it rotates. We may call 10 pi radian per second angular velocity. And this is usually symbolised by an ω. However, we may define angular velocity as a change in angle divided by time. So, based on the results of the computation, we may conclude that ω is equal to the speed for which we are employing v divided by the radius.
Angular velocity formula with frequency
An object’s angular velocity is the rate at which its angular location changes with respect to time. The following formula expresses an essential link between angular velocity and frequency: The product of frequency and the constant 2pi yields angular velocity. The constant 2pi is derived from the fact that one rotation per second corresponds to two pi radians per second. In other words, whenever an object completes one full rotation every second, it rotates at a rate of 2 pi radians per second. Angular velocity may also be expressed in terms of period, which is the amount of time in seconds required for an object to complete one full rotation.

1: Determine the angular frequency of an oscillating object having a 30 second time period.
Solution: As stated previously
T = 30 seconds
Using the formula,
ω=2πT
Changing the values,
ω=2π30
= 360°30
ω=12°sec−1
As a result, the angular frequency is 12°/sec.
Angular velocity formula examples
Q1) Determine the angular velocity of a 0.500 m radius bus tyre travelling at 10.0 m/s (about 36 km/h).
Solution:
Given:
v= 10.0 m/s
r= 0.500m
We are aware that
v= r ω
or
ω = v/r
We obtain by substituting the supplied numbers in the preceding equation:
ω= 10.0 m/s /0.500m = 20 rads^-1
When we cancel out the units in the previous computation, we obtain 20.0/s. However, the angular velocity must be measured in rad/s. Because radians are unitless, we can simply plug them into the angular velocity solution.
Q2) On the highway, an automobile wheel with a radius of 20 inches revolves at eight rotations per second. What is the tire’s angular velocity?
Solution:
The angular velocity may be calculated using the following equation:
ω= θ/t
We multiply by two since a full rotation (360°) equals two because the automobile has completed eight rotations each second.
We obtain by substituting the numbers in the equation,
ω= 16 pi radians/1 s = 16 pi rads^-1
As a result, the tire’s angular velocity is
16 pi rads^-1
Some frequently asked questions
What is the angular velocity?
The rate of change of an angle is defined as angular velocity. In symbols, this is ω=ΔθΔt ω = Δ θ Δ t , where an angular rotation occurs in time delta t. The angular velocity increases as the rotation angle increases in a certain length of time. Radians per second (rad/s) are the units for angular velocity.
How do you find angular velocity with revolutions?
One revolution is 360 degrees and there are 60 seconds per minute. AV in degrees per second translated to revolutions per minute by multiplying the angular velocity by 1/6. If the AV is 6 degrees per second, the rpm is 1 revolution per minute, since 1/6 multiplied by 6 equals 1.
What is an example of an angular velocity example?
It is less frequent than linear velocity since it only applies to things travelling in a circular route. An example of angular velocity is a roulette ball on a roulette wheel, a race vehicle on a circular circuit, and a Ferris wheel.
What is the formula for linear velocity?
The linear velocity of an item is determined by the distance it travels in relation to the time it takes. v = x/t is the linear equation or linear velocity formula. Where v denotes linear velocity.
How do you find angular velocity with radius and time?
Angular speed: ω=θ t, where ω is the angular speed symbol, θ is the angle of rotation represented in radians, and t is the time required to complete the revolution.
Linear speed: v=r ω, where v denotes linear speed, r denotes radius, and ω is the angular speed.
What is the difference between angular velocity and linear velocity?
Angular velocity is the rate of change of a spinning body’s angular location. The rate of change of displacement with respect to time when an item moves along a straight route is linear velocity.
What is the formula for revolution?
To do so, apply the following formula: rotations per minute = speed in metres per minute / circumference in metres. Using the same example, the number of revolutions per minute is equal to: 1,877 / 1.89 = 993 revolutions per minute.
What is the average angular velocity formula?
A rotating rigid body’s average angular velocity is defined as the ratio of angular displacement to time interval.
ω average= delta θ/delta t
=θ 2 – θ 1/ t 1 – t 2
What is the angular velocity formula?
ω = 2 pi N over 60 rad per second is the angular velocity formula. We know that the velocity formula in linear motion is the general formula; velocity is just the distance upon the time. If your heart beats twice in one second, the velocity of your body in linear motion is two minutes per second. Assume we apply this approach to angular motion as well, thus the angular displacement unit per second time. So, if your body is rotating, let N be the rpm of the body. The rpm abbreviation stands for rotations per minute. If we want per second, we must divide by 60.