The density of matter is simply defined as mass per unit volume. Density means the amount of matter present in a unit volume of a substance. The magnitude of density shows how compacted or packed or rared a substance is. Calculating density is pretty easy as we only have to follow the basic math formulae. But while calculating density we have to remember that various factors can influence the density of a matter. Especially where gases are concerned, the density can change due to temperature. The density can also change due to stress, pressure, and many other factors.

Calculating Density Formula
The density of a material shows how dense that material is within a specific given area. A material’s density is defined as the mass contained per unit volume. We define a material’s density as the mass contained per unit volume.
It is a characteristic physical property for a particular object. While it is unique, it does change with changes in physical conditions around the matter. Greek scientist Archimedes is the one who discovered the principle of calculating density.
Calculating density is pretty easy if you know the formula. Alongside that, you also need to understand the units related to it. The symbol ρ represents density. Density can also be represented by the letter D.
Density = Mass / Volume
Therefore, ρ = m / V
In the given formula ρ stands for the density of the substance. While m stands for the mass of the substance, V stands for the magnitude of the volume of the material.
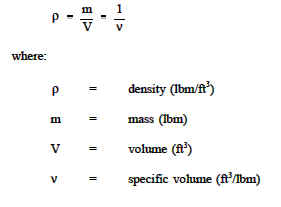
Calculating Density Units
Though the SI unit of density is kg/m³, for our benefit we use g/cm³ for solids. We also use g/ml for liquids and g/L for gases. We can explain density as the relationship between the mass of the substance and the volume it covers. Qualitatively, calculating density shows how much heavy a substance is at constant volume.
Different substances have different densities. Therefore, the same volume of different substances has different weights on measurement.
The SI unit of density is kilograms per cubic meter (kg/m3). It combines the SI units of mass and volume.
The SI unit of mass is kilogram (kg) while the SI unit of volume is cubic meter (m3). Therefore, density denoted by ρ has the units of mass/volume that is kg/m3.
As far as the other density units are concerned, metric tons and liters are also used even though they are not part of the SI system. Some other units of density include:
- gram per milliliter (g/mL)
- metric ton per meter cube (t/m3)
- kilogram per liter (kg/L)
- megagram (metric ton) per meter cube(mg/m3)
- gram per centimeter cube (g/cm3) [1 g/cm3 = 1000 kg/m3]
- kilogram per decimeter cube (kg/dm3)
Added to this, in the CGS system density (ρ) is measured in gram per centimeter cube (g/cm3).
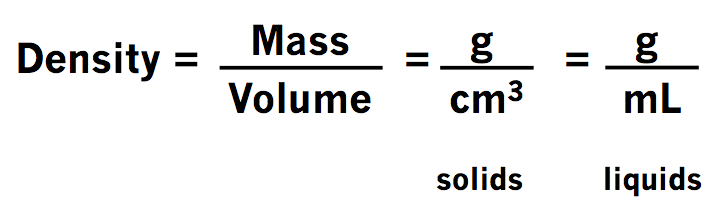
Calculating Density from Mass and Volume
The density of a material shows how dense that material is within a specific given area. A material’s density is defined as the mass contained per unit volume. Calculating density is pretty easy if you know the formula. Alongside that, you also need to understand the units related to it. The symbol ρ represents density. Density can also be represented by the letter D.
Density = Mass / Volume
Therefore, ρ = m / V
In the given formula ρ stands for the density of the substance. While m stands for the mass of the substance, V stands for the magnitude of the volume of the material.
Though the SI unit of density is kg/m³, for our benefit we use g/cm³ for solids. We also use g/ml for liquids and g/L for gases. We can explain density as the relationship between the mass of the substance and the volume it covers. Qualitatively, calculating density shows how much heavy a substance is at constant volume.
Calculating Density Techniques
Density is simply a measurement of how compact matter is packed within itself. The density of a material shows how dense that material is within a specific given area. We define a material’s density as the mass contained per unit volume.
Calculating density is very easy. You need to know the mass of the substance and the volume it occupies. Density is mass per unit volume. So divide the mass by the volume. Therefore, your density is mass/volume.
Calculating density is a bit tricky with liquids. We have to measure the liquid mass on a weight. And hence, also subtract the weight of the empty container from it. Therefore, we will get the value of the mass.
Read Also: Decimal to Fraction | Online Calculator with Examples,
We cannot calculate the density for an entire mixture. Since the particles in the mixture are not distributed in a uniform nature. In addition to this, the mass changes throughout the volume. For a homogeneous mixture, calculating density needs two simple measurements. Though it is unless you have a hydrometer that can compute the density directly.
Calculating Density Practice Problems
Question: Take two boxes with the same volume. Fill the first box with x balls and the second box with 5x balls. If the mass of each ball is equal, which box would weigh more?
Solution:
The box that has more balls inside it has more of the mass per unit of its volume.
Here the first box contains x number of balls and the second box contains a 5x number of balls. Since the number of balls in the second box is 5 times the first box, the second box would weigh more. We call this property of matter its density.
Question: If you find a shiny stone, a carbon allotrope with a volume of 0.042 cm³ and a mass of 0.14 g, is it graphite or diamond? The density of graphite is 2.266 g/cm3 and the density of diamond is 3.51g/cm3.
Solution:
Given,
Volume of the shiny stone = 0.042 cm³
Mass of the shiny stone = 0.15 g
Density of a graphite = 2.266 g/cm3
Density of a diamond = 3.51 g/cm3
Now you have to use the density equation to solve for m, mass of graphite and for the mass of a diamond.
ρ = m/V
m = ρV
m = 2.266 g/cm³ x 0.042 cm³ = 0.0951 g for graphite
m = 3.51g/cm3 x 0.042 cm³ = 0.1474 g for diamond
The mass of the shiny stone you found is identical to the mass of a diamond. Therefore, it is most probably a diamond.

Calculating Density of States
In the domains of solid-state physics and physics of condensed matter, we need this concept. The density of states (DOS) of a system defines the ratio or proportion of states that are to be occupied by the system at each level of energy.
We can define the density of states as D(E)=N(E)/V. Where N(E)δE is the number of states in the system of volume V. Among these is only the states whose energies lie in the range from E to E+δE.
It is mathematically or physically shown as a distribution by a probability density function. It is usually an average over the space and time domains of the various states. All these are the states that the given system contains. We can also map the density of states directly to the dispersion relations of the properties of the system.
High Density of State (DOS) at a specific energy level means that many states are available for occupation. Therefore, this is the conclusion.
Calculating Density of Crystal Lattice
Every solid state matter has a unit cell. The unit cell is the most basic repeating unit of a lattice.
Now for us to calculate the mass of one unit cell of a lattice. We, hence, add up the masses of all the atoms included within that particular unit cell. The number of atoms will depend on the type of cell the lattice has. So to get the mass of a unit cell we will multiply the number of atoms “n” into the mass of each atom “m”.
The Mass of the unit cell = n × m (n is the number of atoms and m is the mass of each atom)
But now the question arises, what is the mass of an atom? Well, we can even simply represent this in terms of its Avogadro Number (NA). That is, the number of units in one mole of any substance and the molar mass of an atom. So we can henceforth calculate the mass of an atom as;
The Mass of an atom = Molar Mass / NA
So the formula of the mass of unit cell becomes; nM / NA
(Where n is the number of atoms, M is the molar mass and NA is Avogadro’s number)
Volume of the unit cell is easy to find as we know that the unit cell is a cube.
The Volume of the unit cell = a3 (where a is the length of a side of the cube)
Therefore the density of the unit cell is Mass/Volume.
The Density of the unit cell =
(where n is the number of atoms in a unit cell, M is the molar mass, a is the side length of the cubic unit cell and NA is Avogadro’s number)
Calculating Density of Mixtures
A mixture can be either homogeneous or heterogeneous. We cannot calculate the density for an entire mixture. Neither can we calculate the density for a heterogeneous mixture. Since the particles in the mixture are not distributed in a uniform nature. In addition to this, the mass changes throughout the volume.
For a homogeneous mixture, calculating density needs two simple measurements. Though it is unless you have a hydrometer that can compute the density directly.
Firstly, measure the volume of the homogeneous mixture. If it is a liquid, pour some of it into a graduated cylinder. Hence, read and also record the volume. If the mixture is solid, then pour some water into a beaker or graduated cylinder. Hence, read the volume and then place the solid in the water. You must make sure the solid mixture is completely covered. Therefore, read the new volume and subtract the original volume to find the difference. This difference is henceforth, the volume of the solid mixture.
Now place the mixture on a mass scale and even record its mass. If it is a liquid mixture, do not forget to subtract the mass of the container housing the liquid.
Now that you have the data for both mass and volume. You can also divide them to get the magnitude of density.

Calculating density of a liquid
To measure the mass, put the liquid in a container and weigh it. Subtract the weight of the empty container from it. We, therefore, get the volume from the cylinder in itself. Henceforth, divide the mass by the volume and you will get the density.
Calculating density of a gas
It is simple. For the volume consider the volume of the container for the gas. The mass is the weight of the gas jar with the weight of the empty container subtracted. Hence, divide the two. Therefore, you will obtain the density of the gas.
FAQs on calculating density
1. How can I calculate density?
Calculating density is very easy. You need to know the mass of the substance and the volume it occupies. Since density is mass per unit volume, it is simple. Therefore, divide the mass by the volume and you have your density calculated.
2. What are the three steps of calculating density?
The three steps are;
- Find the mass of the substance
- Find the volume of the substance
- Divide the mass by volume
3. How do you manually calculate density?
Calculating density is pretty easy if you know the formula. Alongside that, you also need to understand the units related to it. The symbol ρ represents density. We can also represent density by the letter D.
Density = Mass / Volume
Therefore, ρ = m / V
4. How do you find density with grams and mL?
There is a unit of density for gm/mL. But if you want to convert it into the SI system then consider the following.
1 mL = 10-6 m3 and 1 g = 10-3 kg
Therefore, 1 gm/mL = 103 kg/m3. You can also use this conversion technique to aid your calculation.
5. Calculate the density of a liquid if it has a mass of 1250 kg in a volume of 1 m3.
Given, mass = 1250 kg and volume = 1 m3. Density is given by the formula:
Density = Mass/Volume;
Therefore; ρ = 1250/1 = 1250 kg/m3