Of course, derivatives are a very tough nut to crack. So, students often try to skip these lessons because it intimidates them thoroughly. Now, differentiation has a few formulas which are actually the basic ideas one must have to solve these sums. Once you get the hang of it, they actually seem quite easy.
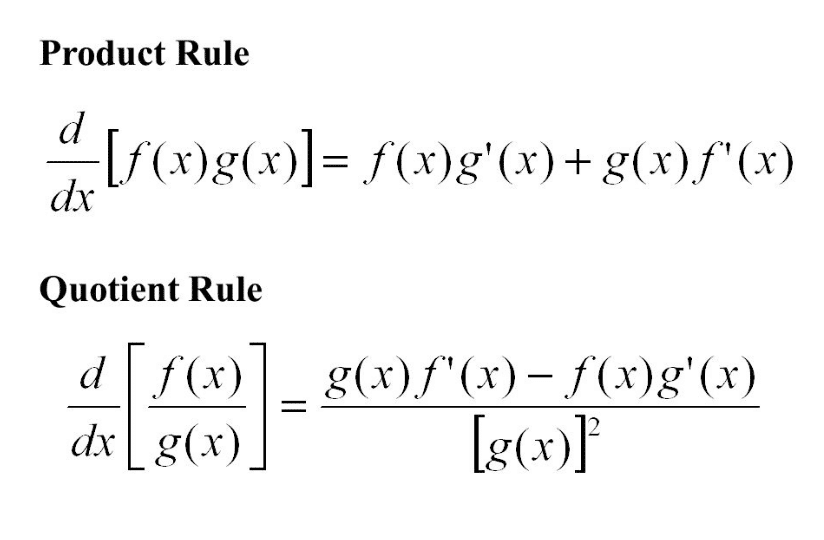
So, it is important that you learn the differentiation chain rule, addition rule, subtraction rule, quotient and product rule formula. However, you have to apply the chain rule most often.
But, the quotient and product rule formula also comes in very handy at times.
Quotient and product rule formula
A function might be a sum, product, or quotient of simpler functions. so, we can differentiate it on the grounds of simple functions. And, their derivatives using the sum, quotient and product rule formula.
The product rule states that if P is a product of discrete functions f and g, then
P(x) = f(x)*g(x).
Thus,
P’(x) = f(x) g’(x) + g(x) f’(x).
The quotient rule states that if Q is a quotient of discrete functions f and g, then Q is a quotient of differentiable functions f and g.
Q(x) = f(x) / g(x).
Thus,
Q’(x) = [g(x) f’(x)-f(x) g’(x)] / g(x)^2.
The product and quotient rules, as well as the constant multiple and sum rules are very important. In fact, they allow us to find the derivative of any variable that includes sums, fixed multiples, products, and quotients of core parts.
Now, we will have a look at some more advanced features of differentiation. To recap, we know that:
The constant multiple of the derivative is the fixed multiple of the derivative.
A sum’s derivative is the total of its derivatives.
The variance of the derivatives is the derivative of the derivatives.
But, we see that:
The derivative of f(x)g(x) is not the derivative’s products.
Also, similarly the derivative of a quotient f(x) / g(x)is not the derivatives’ quotient.
At the same time, the derivative of the functions of type f(g(x)) is not the derivatives’ composition.
What is the quotient rule formula?
The quotient rule is a way in calculus for getting the derivative of the function, i.e., the ratio of two differentiable functions.
Let us consider a function, say, f(x) = g(x) / h(x). Of course, g and h are differentiable and h(X) is not equal to 0.
According to the quotient rule,
f’(x) = [g’(x) h(x)-g(x) h’(x)] / h(x)^2.
In the article on the quotient and product rule formula, we now focus on the quotient rule.
Quotient Rule is a method in Calculus for calculating the derivative (differentiation) of a function in terms of the ratio of two differentiable functions. It is an official rule used in differentiation situations when we have one function in the numerator and the other one in the denominator. The quotient rule reflects the concept of the derivative’s limit. Keep in mind that the quotient rule starts with the lowest function and continues with the lowest function squared.
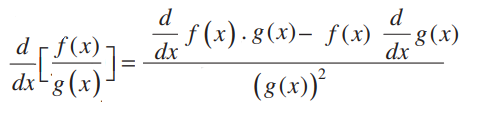
A Quotient rule is almost the same as a product rule in Calculus. A Quotient Rule is defined as the ratio of the amount of the denominator multiplied by the derivative of the numerator function to the square of the denominator function. In a word, the quotient rule is a means of distinguishing the division of functions or quotients. In mathematics, we know it as the quotient rule differentiation. Read Also: Derivative of Tangent x: Formula, Rules, Examples
In tune with the first principle of derivatives, we all know that, we can express a derivative as:
f’ (x) = lim [f(x+h) – f(x)] / h.
In fact, the proof for the quotient rule (using the first principle) is as follows:

Now, have a look at this proof. It is sure to clear your confusions regarding the origin of the quotient rule.
How do you use the quotient rule
In this article, we discuss the quotient and product rule formula in general. Here, we focus primarily on the quotient rule.
So far we have tried to learn the quotient and product rule formula. But, now we shall focus on when and why we should use this rule in the context of derivatives.
When taking the derivative of the quotient of two functions, people use the Product Rule. Thus, it is that simple.
Now, we shall go ahead and write the product rule in words.
According to the Quotient Rule, the derivative of a quotient equals the denominator times the numerator’s derivative less the numerator times the denominator’s derivative, all divided by the denominator’s square.
Even though this might seem a bit tough, in reality, that is not the case. In fact, once you start applying this rule in sums you can very easily understand it all.
Now, we shall list an example for you to learn how to apply the quotient rule:
Let us use the function t = (y^2 + y – 2) / (y^3 + 6).
Thus, in the next step we write it as:
t’ = [(y^3 + 6) d/dx (y^2 + y – 2) – (y^2 + y – 2) d/dx (y^3 + 6)] / (y^3 + 6)^2
Or, [(y^3 + 6)(2y + 1) – (y^2 + y – 2) 3x^2] / (y^3 + 6)^2
Or, [(2x^4 + x^3 + 12x + 6) – (3x^4 + 3x^3 – 6x^2)] / (y^3 + 6)^2
Or, [- x^4 – 2x^3 + 6x^2 + 12x + 6] / (y^3 + 6)^2.
Thus, the answer looks like the last line. So, you can see how it is so easy to make calculations of derivatives using the quotient rule.
When to use the product and quotient rule
By now, you know how to use the quotient and product rule formula to solve certain derivatives.
Here, we can make a list. That will make it easier for you to remember when and how we should apply the derivative rules.
- Write down the constant, constant multiple, and power laws.
- To combine derivatives, use the sum and difference methods.
- To find the derivative of a function product, you need to use the product rule.
- To get the derivative of a ratio of functions, you have to use the quotient rule.
- Adapt the power rule to also include negative exponent functions.
- To obtain the derivative of a quadratic , a polynomial or rational function, combine the differentiation rules. However, this differs on a case by case basis. And, you need to learn when to apply which.
Thus, now you need to focus on the quotient and product rule formula alone. If you look at a generic equation, it usually looks like this:
y=f(s),
where f(x) is a function defined strictly in terms of s. It could be multiplication of s, division of s, or any possible function. You can detect them as follows:
Function multiplication. For instance, (s-1) (s-2). You could see that two separate functions of s, namely, (s-1) and (s-2) are multiplied here.
Now, suppose you need to divide any two functions. For instance, (s – 5) / (s – 2). You can check that two separate functions of s, namely, (s – 5) and (s – 2) are divided here.
So, anytime there is a product of two factors, you have to use the product rule. And, when there is a division, you have to use the quotient rule. If a function has both multiplication and division rules, simply apply both rules.
How to do product and quotient rule?
Optimization, as one of the fundamental aspects in many machine learning techniques, makes use of derivatives to find how to update a model’s parameter values in order to maximize or minimize an objective function. Thus, you have to learn the concepts and the quotient and product rule formula in order to use them easily.
If we had to seek each derivative from fundamental principles, that would be very tedious and time-consuming. As a result, for hugely tough functions, keeping such rules on hand to get their derivatives will be very important. So, it becomes important to learn the quotient and product rule formula.
You need to learn to apply two things:
- How the product rule helps us get the derivative of the function when you define it as the product of two (or more) other functions.
- The quotient rule lets us calculate the derivative of the function that is the ratio of two separate differentiable functions.
Assume we now have a function, f(x), whose derivative we want to find. Now, it can be the product of two additional functions, u(x) = 2x^2 and v(x) = x^3:
f(x) = u(x) * v(x) = (2x ^ 2) (x ^ 3)
To begin learning how to get the derivative of f(x), let us first find the derivative of the mix of u(x) and v(x) directly:
(u(x) v(x)) = ((2x ^ 2) (x ^ 3)) = (2x ^ 5) = 10x ^ 4
Now think about what would happen if we had to find the derivatives of the functions singly first and then multiply them:
u'(x) v'(x) = (2x ^ 2)’ (3x ^ 2) = (4 x) (3x ^ 2) = 12x ^ 3.
Of course, the results do not match. This is due to the product rule.
How to use the quotient rule to find derivatives?
The next time you solve derivatives, keep a note of the quotient and product rule formula. Similarly, the quotient rule directs us on how to get the derivative of a function, f(x). Also, this is the case when there is the ratio of two differentiable functions, u(x) and v(x):
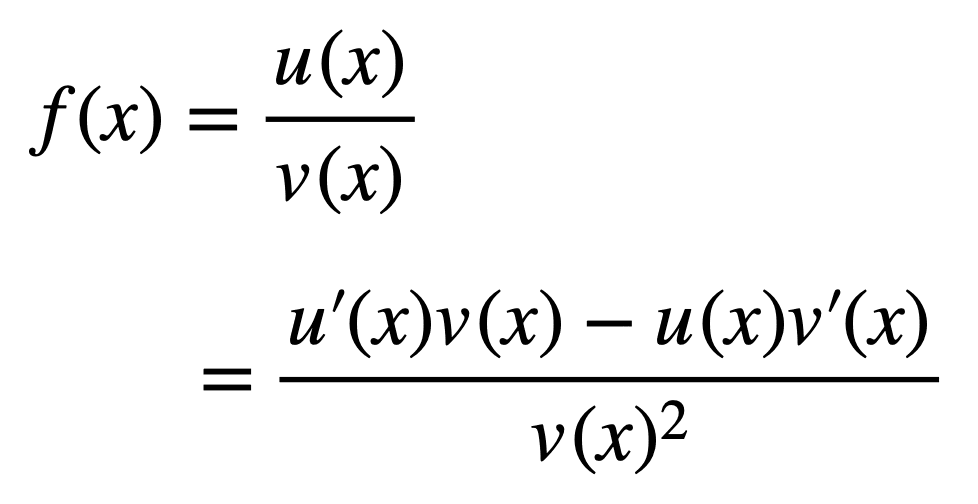
The quotient rule can be derived from first principles in the same way as the product rule. That is, by starting with the idea of a derivative and using the rules of limits. We can also find another route and get the quotient rule from the product rule. This time, let’s take the following path:
We can use the product rule on u(x) to get:
u’(x) = f’(x) v(x) + f(x) v’(x)
Now, it is time for us to solve back for f’ (x):
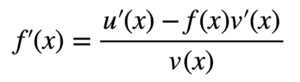
Now, for the final step to reach the quotient rule formula:
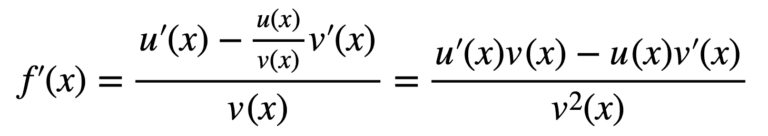
Product and quotient rule calculator
Much the same way as any mathematical operation, you can also use an online calculator to apply quotient and product rules to the functions. In fact, it is also used very often. The online calculator makes the process faster as compared to the handwritten method, a lot faster. And, also a more accurate process.
Thus, when you are not able to apply product or quotient rules to a function, go ahead and try to use the calculator for the same.
The quotient rule is used in mathematics to get the derivative of a function. When the function is the ratio of two analytic functions, you can use this method. Follow these steps to use the quotient rule calculator:
Firstly, type the numerator and denominator functions into the suitable data fields.
Secondly, to get the derivative, click the “Submit” button.
Lastly, in the new window, you can find the derivative of the input function.
A product rule is used in calculus to contrast functions when one value is multiplied to another function. In fact, it is a formula to calculate the derivative of a function.
Even if you have x and y functions, such as xy. Use the product rule to define them as two distinct functions. Perform the following steps to use the product rule calculator:
Step 1: Type the function into the input box.
Step 2: Then, to arrive at conclusions, click on the “Submit” button.
Step 3: Finally, in the new window, the calculator will display the differentiation of the given function.
Now, we shall provide you the link for the product rule calculator as well:
Quotient and product rule formula FAQs
1. How do you know when to use the product or quotient rule?
Ans: To find the derivative of a function product, you have to use the product rule. To get the derivative of a division of functions, you can use the quotient rule.
2. How does the product rule work?
Ans: Essentially, it is quite simple. You just have to add f multiplied by the derivative of g to the derivative of f multiplied by the derivative of g.
3. Can you use the product rule instead of the quotient rule?
Ans: Actually, it is a trick of differentiation. Like an experiment, you can try to use that idea to get the quotient rule. They are, indeed, the same. If you don’t need to simplify, we feel that way is a lot easier.
4. Why do we need the product rule?
Ans: In calculus, the product rule is used to find the derivative of function products. In fact, the product rule formula is stated for the product of two functions. But, you can also extend it to the product of three or more functions.
5. What is the power of product rule?
Ans: When you multiply more than one variable and raise it to a power, we employ the force of a product rule. According to the power of a product rule, we can reduce a power of a power by multiplying the exponent variables while having the same base.
6. Who invented the product rule?
Ans: Gottfried leibniz was the person who invented the product rule. However, this rule enables us to obtain derivatives that we do not want (or cannot) multiply fast.
7. When taking a quotient to a power what do we do with the exponents?
Ans: Of course, we can take the example of the quotient of powers property. It states that when dividing powers with the same base, we just delete the exponents. Raising a quotient to a power raises both the numerator and denominator towards the power. Thus, when you raise an integer to a zero power, the result is always 1.
8. Is product rule a chain rule?
Ans: Use the product rule if the main operation on the functional forms is multiplication. On the other hand, you can use the quotient rule if the end operation on the functions is division. Finally, you should use the chain rule if the last action on variable quantities is to apply a function.
9. Why is the quotient of powers property valid?
Ans: To ease the difficulty of division like phrases using exponents, adopt the Quotient of Powers Rule. When dividing items with the same base, this rule says that you should simply subtract their exponents to get your answer.
10. What is the constant multiple rule for derivatives?
Ans: According to the Constant multiple rule, the derivative of a steady multiple by a function equals the constant multiplied by the function’s derivative.
11. How do you know when to use the product rule?
Ans: In general, we use the chain rule to differentiate a ‘function of a function,’ such as f(g(x)). When differentiating two functions that are expressed as a product together, such as f(x)g(x), we apply the product rule.
12.How do you divide derivatives?
Ans: Firstly, multiply g(x) by the derivative of f. (x).
Then, deduct the product of f(x) multiplied by the derivative of g from that product (x).
Finally, for the last step, you multiply those variables by g(x) squared.