So, before we go into the complex stuff and the centripetal acceleration formula itself, let us start at the most basic level. What is centripetal force? So, centripetal force is one of the two key forces that are responsible to keep a body moving in a circular or a curved path. Moreover, it acts towards the center of rotation. Therefore, to balance it, the centrifugal force acts outwards from the center of rotation. These two are together jointly called the Coriolis forces. Hence, it is their perfect balance that keeps a body in motion in a curved path. So now the next question should ideally be what is centripetal acceleration? Therefore, centripetal acceleration is simply the acceleration of a body that is moving in a curved or circular path.
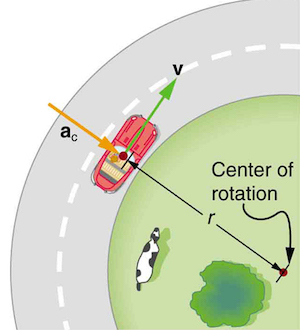
So, we already know that velocity is a vector quantity. Therefore, it is the magnitude of the speed of a moving body with the direction. Now, when a body is in motion on a circular path, its direction is changing continuously. Therefore, its velocity is also changing. Now, we all know that acceleration in physics is the rate of change in the velocity of a moving body. Therefore, when the velocity changes, it produces an acceleration. This is what we will be dealing with- centripetal acceleration.
Read Also: What is Molar Mass? – Definition, Formula & Examples
Therefore, let us take a quick look at the centripetal acceleration formula now. It is ac = v^2 / r.
So, here ac is centripetal acceleration, v is the velocity of the body in motion and r is the radius of the circular path. Therefore, you realize that the formula is just like normal acceleration. However, the only difference is in this case, instead of straight distance, you have the radius because the motion is circular. Let us take a look at its derivation.
Centripetal acceleration formula derivation

We will see the derivation of the centripetal acceleration formula in reference to this figure.
So, we already know that the direction of centripetal acceleration is toward the center of curvature, but we need to find its magnitude. Moreover, if you look closely you will see that the triangle that the velocity vectors form and the one that the radii r and Δs form are similar. So, both these triangles are isosceles. Therefore, the two equal sides of the velocity vector triangle are the speeds v1 = v2 = v.
Moreover, if we apply the theorems of similar triangles here, we will get-
Δv/ v = Δs/ r.
Therefore, acceleration Δv/ Δt.
Hence, let us first solve the expression to get Δv. So, we have-
Δv = Δs/ r * v
Now, if we divide the entire equation by Δt, we get-
Δv/ Δt = Δs/ Δt * v/ r
Now, we already know that Δv/ Δt gives the acceleration which in this case is ac. Moreover, we also know that Δs/ Δt is velocity or v.
So, summing up we have-
ac = v^2/ r.
So, this is how we derive the centripetal acceleration formula. The key to this is the knowledge of similarity in triangles. However, there is another way to express it. Let us see how.
Centripetal acceleration formula in terms of omega
So, if you are a high-school student in physics, you already know that in rotational dynamics, omega or ω stands for angular velocity. Since centripetal acceleration is of a body in a circular path, angular velocity matters here. Moreover, we get angular velocity or ω simply by dividing normal velocity by the radius of the circular path. Therefore, ω = v/r. So, we have v = rω.
Therefore, by substituting the values in the centripetal acceleration formula we have-
ac = ( rω)^2 / r. Moreover, this is the same as ac = rω^2.
So, finally, we have, ac = rω^2.
Therefore, this is how we represent the centripetal acceleration formula in terms of angular velocity or omega.
It is useful to know both the formulas because you do not know where you will need which application. Therefore, in some cases, you might have normal velocity and some angular velocity. However, you should be able to calculate the centripetal acceleration no matter what.

Centripetal acceleration formula in vector form
So as we get up in high school, we learn how to represent vector quantities in vector form.
Therefore, in the figure that we see above, as the particle moves counterclockwise in time
Δt on the circular path, there is a movement of the position vector. So, it moves from r (vector)(t) to r (vector)(t + Δt). However, in the process, as the tangent of the velocity vector changes, its magnitude remains the exact same. Moreover, the velocity vector v(vector)(t) is perpendicular to the position vector r(vector)(t). Moreover, the triangles that the velocity vectors and position vectors form are also similar.
Now, we already know-
I r(vector) t I = I r(vector) (t + Δt) I and also
I v(vector) t I = I v(vector) (t + Δt) I
So from here on, we have Δv/ v = Δr/ r.
Moreover, from here on if we follow the derivation that we have seen just above, we will get the same centripetal acceleration formula. Therefore, it remains the same but this is how you take into consideration the dimension of direction in the entire process.
Centripetal acceleration formula class 11
Now, in the 11th grade, rotational dynamics is something that we hear for the first time. So, most of us come across the centripetal acceleration formula also for the first time. Therefore, the definition, the formula, the derivation- all of these might be very overwhelming and confusing for many of us. So, let us take a look at some examples that will help us understand the concept way better.
Question 1
Calculate the centripetal acceleration of a point 7.50 cm from the axis of an ultracentrifuge spinning at 7.5 × 104 rev/min. Determine the ratio of this acceleration to that due to gravity.
Answer: So let us solve it now. To begin with, for converting 7.50 × 104 rev/min to radians per second, we make use of the standard that one revolution is 2π rad and one minute is 60.0 s. Now, we already know that the centripetal acceleration formula is ac = rω^2. Therefore, at first, we are going to convert 7.50 cm to meters. Moreover, we are going to substitute the known values. So, this gives ac = (0.0750 m) * (7854 rad/s)2 = 4.63 × 106 m/s2.
However, you should take note of two things here. First, the unit of angular and linear velocity is not the same. However, the final unit of centripetal acceleration remains the same as normal linear acceleration. Secondly, you have to discard the unitless radians so that you can get the correct units for centripetal acceleration. Moreover, this is going to help us in doing the ratio with normal gravitational acceleration. Now, taking the ratio of ac to g, we get-
4.63 × 106 m/s^2 / 9.80 m/s^2 = 4.72 x 10^5.
So, the final ratio that we get is 4.72 x 10^5.

Question 2
What is the magnitude of the centripetal acceleration of a car following a curve of radius 500 m at a speed of 25.0 m/s (about 90 km/h)? Compare the acceleration with that due to gravity for this fairly gentle curve taken at highway speed.
Answer. So now let us see how we can solve the sum. Therefore, we can simply place the values in the centripetal acceleration formula and we will get the final value of acceleration. Hence, ac = v^2/ r. Since the units are in m and m/s, we do not need to convert anything. So, it is much easier compared to the previous sum. Therefore-
ac = (25 m/s)^2 / 500 m = 1.25 m/s^2.
So, this is our centripetal acceleration. Now, we have to find the ratio between it and the normal acceleration due to gravity. Therefore, let us take a look at it.
ac / g = (1.25 m/s^2) / (9.80 m/s^2)
So, the ratio that we finally get is 0.128. Against the previous case, this does not happen in a science lab but on the road. So, this is quite a considerable amount of acceleration.
Centripetal acceleration formula calculator
Having everything online has a lot of benefits. So, these days even for minor inconveniences, you can resort to the internet. Therefore, in case you have still not got the hang of the centripetal acceleration formula well enough, you can use a calculator. The calculator will help you not just to do the sums. It is going to help you understand the process better such that you can do the sums yourself later on. Moreover, it is an excellent device for verification if you are not sure of your answer. This makes sense because we are human beings and are prone to making minor mistakes while calculating manually. Here, we will be using the centripetal acceleration calculator from Byju’s.

Step 1 to use the centripetal acceleration formula calculator
So, access the calculator from Byju’s first. Click on Byju’s and you will directly land on the page of their calculation. Once you have landed on the page, you will find the centripetal acceleration formula for better understanding. Then you have to input the acceleration, the velocity, and the radius values all manually. However, remember the velocity here is linear velocity and not angular. Moreover, the best part about this is the quantity whose value you want to find, you enter an x. So, in that way, it is not necessary to find out acceleration only. From the centripetal acceleration formula, you can find the velocity or the radius as well.
Step 2 to use the centripetal acceleration formula calculator
Now, we have already seen examples where we needed to find out the value of centripetal acceleration. So, for a change, let us see how to find the velocity from the radius and centripetal acceleration values. Hence, enter the respective values in the boxes beside and in velocity, enter x. Let us say, we take the acceleration to be 1.25 m/s^2 and the radius to be 500 m. Now, after you enter the values, click the “calculate the unknown” bar. So you will find this right below the box where you enter the value of the radius.
Step 3 to use the centripetal acceleration formula calculator
It hardly takes a fraction of a second to complete the calculation. Soon, below the calculation bar where there is the box that will show the value of x, the value appears. Therefore, in this case, this is 25. Since it is velocity, it becomes 25m/s
Let us cross-check.
Now, we already know that the centripetal acceleration formula = v^2/ r
Or, v = (ac * r) ^ (½)
So, v = (1.25 * 500) ^ (½)
Therefore, v = (625) ^ (½) = 25 m/s.
So, the calculator works perfectly.
Centripetal acceleration formula with mass
As per the second law of motion, Newton states that the net force of any object is the multiplication of its mass and acceleration or is the mass times acceleration. Therefore-
F = ma
Let us see how.
Therefore, we are going to consider an object of mass m that is moving along a straight line with an initial velocity u. However, after a certain time t, with a constant acceleration, the final velocity becomes v. So, the initial momentum p1 is-
p1 = m × u
Moreover, the final momentum p2 is-
p2 = m × v
So, the change in momentum due to change in velocity is-
p2 – p1 = (m × v) – (m × u)
Or, p2 – p1 = m (v – u)
However, we already know that the rate of change of momentum with respect to time is directly proportional to the force applied on the object.
So, we can say the applied force F ∝ [m (v – u)] / t
Now, the rate of change of velocity or (v – u) / t is acceleration. Therefore, we can say
F ∝ m × a
So, F = k * m * a where k is the proportional constant.
Now, consider uniform circular motion. Here the acceleration is centripetal acceleration ac . So, centripetal force or Fc = m * ac. Therefore, ac = Fc / m.
So, this is the centripetal acceleration formula with respect to mass.

Centripetal acceleration formula units
So, we have already seen the units of centripetal acceleration while solving the sums. However, we need to understand a few things better to see where the unit comes from.
Hence, we already know the unit of radius or distance is meter. Next, the unit of linear velocity is m/s. Therefore, if we use the centripetal acceleration formula now, we have- ac = v^2 / r
So, the unit of ac = m^2 / (s^2 * m)
So, we have simply m/s^2 which is the same as normal linear acceleration. Now, if we consider the formula in respect to angular velocity, we have-
ac = rω^2
So, by this, the unit of ac would be m * m/s = m^2/s but that is clearly not the case. This is what you need to remember. The units of angular and linear velocity are entirely different because they are different quantities. So, m/s is the unit for normal velocity. Angular velocity is the ratio of normal velocity to the radius. Therefore, its unit is m/ (s * m) or /s alone. Now, let us see if we get the correct unit of ac.
Therefore, unit of ac = m * (s^ -1) ^2.
So, this comes to be m/s^2 just like in the previous case.
Centripetal acceleration formula FAQs
What does centripetal acceleration depend on?
Ans. So, the centripetal acceleration depends on the velocity of the moving particle and the radius of the circular path. This is evident from the centripetal acceleration formula that says ac = v^2/ r. So, here, ac is the centripetal acceleration, v is the velocity of the particular, and r is the radius of the circle.
Does centripetal acceleration depend on speed?
Ans. Yes, it definitely depends on speed, as is evident from the formula. Moreover, it is directly proportional to the speed, or velocity per se. So, as the speed increases, the centripetal acceleration also increases.
What is the relationship between centripetal force and acceleration?
Ans. So, the relation between centripetal force (Fc) and acceleration ac is Fc = m * ac. To know more in detail, check out the “centripetal acceleration formula with mass” section of the article.
Is centripetal acceleration always positive?
Ans. No, not necessarily. It depends on the direction of the moving particle. It can be positive or negative.
Are radial and centripetal acceleration the same?
Ans. Yes, they are the same thing. Because of its direction towards the center of the circle, we also refer to centripetal acceleration as radial acceleration for easier understanding.
NOTE: Throughout the article, ac means centripetal acceleration. It is not any other new quantity. Moreover, it has the same unit as that of linear acceleration as we have already seen.